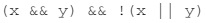
In this case, the expression (x && y) && !(x // y) can be rewritten as (x && y) && (!x // !y). Using De Morgan’s law, this can be further simplified to (!x // !y) && (x && y). This expression is only true if both (!x // !y) and (x && y) are true. However, these two conditions are mutually exclusive. In other words, if one of them is true, the other must be false.
Therefore, the expression (x && y) && !(x // y) can never be true, and it will always evaluate to false.
Here is a truth table that shows the results of evaluating the expression for all possible values of x and y:
| x | y | (x && y) | !(x // y) | (x && y) && !(x // y) |
|---|---|---|---|---|
| True | True | True | False | False |
| True | False | False | True | False |
| False | True | False | True | False |
| False | False | False | False | False |
As you can see, the expression is only false in all cases.